
Class 12 Physics Derivations Chapter 1 Hindi Board 2026
प्रश्न 1. विद्युत फ्लक्स को परिभाषित कीजिए। स्थिर वैदुतिकी मैं गैस की प्रमेय का उल्लेख कीजिए तथा इसे सिद्ध कीजिए ।
उत्तर : विद्युत फ्लक्स – किसी विद्युत क्षेत्र में स्थित किसी काल्पनिक पृष्ठ से पृष्ठ के अभिलंवत होकर गुजरने वाली कुल विद्युत बल रेखाओं की संख्या को ही विद्युत फ्लक्स कहते हैं । इसे ∅E से प्रदर्शित करते हैं ।
Also Read
∅E = E .A
गैस की प्रमेय – इस पर में के अनुसार,” किसी बंद पृष्ठ A से गुजरने वाला विद्युत फ्लक्स ∅E , उस पृष्ठ द्वारा घिरे हुए कुल आवेश q का 1/ε₀. गुना होता है ।”
अतः विद्युत फ्लक्स ∅E = q. 1/ε₀. = q/ ε₀.
परंतु बंद पृष्ठ A से बद्ध कुल वैद्युत फ्लक्स
∅E = ∫ E→ .dA→ = q/ε₀.
जहां ε₀. निर्वात अथवा वायु की वैद्युतशीलता है।
उत्पत्ति – माना कोई विद्युत आवेश+q , किसी बन्द पृष्ठ A के भीतर किसी बिंदु O पर स्थित है । माना पृष्ठ A पर कोई बिंदु P है जिसकी बिंदु से दूरी r है। माना पृष्ठ A पर बिन्दु P के चारों ओर एक अल्पांश क्षेत्रफल dA है। जिसके
संगत क्षेत्रफल वेक्टर dA है ।
जिसकी दिशा बिंदु P पर अल्पांश क्षेत्रफल dA के बाहर की ओर खींचे गाय अभिलंब के अनुदिश है।
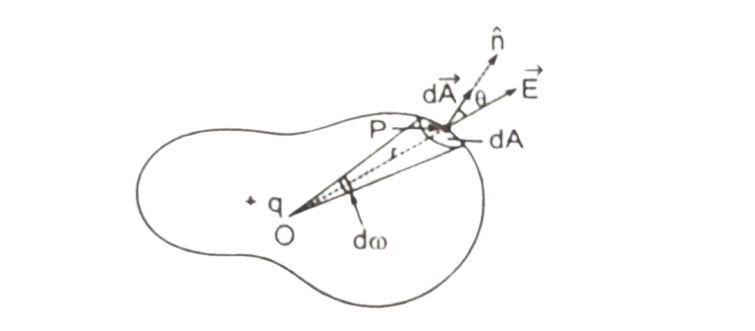
माना बिंदु O पर रख बिंदु आवेश +q के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता
E = q/ 4πε₀.r² (O→F) ——–(1)
यदि विद्युत वेक्टर E तथा क्षेत्रफल वेक्टर dA के बीच कोण θ है तो अल्फाश क्षेत्रफल dA से गुजरने वाला बाहर की ओर दीष्ट विद्युत फ्लक्स
d∅E =EdAcosθ
समीकरण 1 से E का मान रखने पर
d∅E = q/ 4πε₀.r²dAcosθ
= qdAcosθ/ 4πε₀.r²—–(2)
परंतु dAcosθ /r² = dω
जहां dω अल्फाश क्षेत्रफल dA द्वारा बिंदु O पर आंतरिक धन कोण है।
तब समीकरण( 2) से,
d∅E = q/ 4πε₀.dω
अतः बिंदु आवेश q के कारण संपूर्ण पृष्ठ A से बाहर की ओर निकलने वाला विद्युत फ्लक्स
∅E= ∫ d∅E = ∫q /4πε₀.dω
= q /4πε₀. ∫dω
परंतु . ∫dωसंपूर्ण बंद पृष्ठ क्षेत्रफल A द्वारा बिंदु O पर आंतरिक कुल धन कोण है , अर्थात. ∫dω =4π
अतः ∅E=q/ ε₀. यही गॉस प्रमेय है।
प्रश्नानुसार —-
दिया हैं – E = 14 i^ + 13j^ – 5k^ न्यूटन /कूलॉम
A =4j^=0i^+4j^+0k^ मीटर²
∅E= E.A
= (14 i^ + 13j^ – 5k^). ( 0i^+4j^+0k^)
= 12 न्यूटन मीटर²/कूलॉम ।
प्रश्न 2 – किसी विद्युत द्विध्रुव के कारण निरक्षीय (अनुप्रस्थ) स्थिति में किसी बिंदु पर विद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए l
उत्तर: विद्युत द्विध्रुव का निरक्षीय स्थिति पर स्थित किसी बिंदु पर विद्युत क्षेत्र की तीव्रता – माना AB विद्युत द्विध्रुव K
परावैद्युतांक के माध्यम में स्थित है, जिसके सिरे पर +q
आवेश तथा B सिरे पर -q आवेश एक दूसरे से 2l दूरी पर स्थित है ।
इस विद्युत द्विध्रुव के मध्य बिंद O से r मीटर की दूरी पर किसकी निरक्षीय स्थिति में कोई बिंदु P स्थित है। जहां पर विद्युत क्षेत्र की तीव्रता ज्ञात करनी है।
माना+q आवेश -q तथा के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता क्रमशः E1 व E2 हैं।
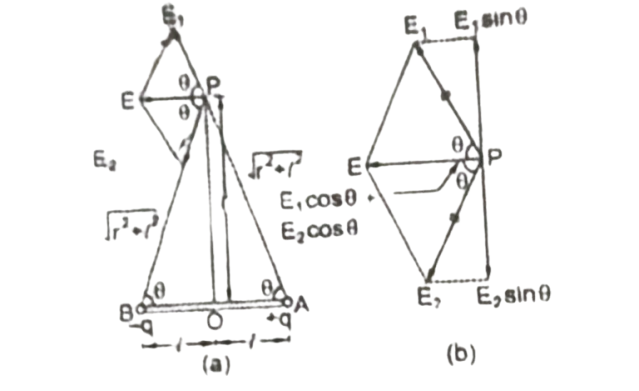
समकोण ∆ AOP तथा ∆BOP से,
AP² = BP² = r² + l²
अथवा AP= BP =√r² + l²
प्रत्येक आवेश से बिंदु P की दूरी √r² + l² हैं।
अतः आवेश+q के कारण बिंदु Pपर विद्युत क्षेत्र की तीव्रता
E1 = q /4πε₀.(r² + l²). ( A →P दिशा में)
तथा आवेश-q के कारण बिंदु Pपर विद्युत क्षेत्र की तीव्रता
E2 = q /4πε₀.(r² + l²). (P→B दिशा में)
चुकीं के मान E1 व E2परस्पर बराबर है परंतु दिशा भिन्न है, अतः E1 व E2 को AB के समांतर तथा लंबवत घटकों में विभाजित करने पर AB के लंबवत घटक E1 sinθ व E2sinθ बराबर वह विपरीत होने के कारण एक दूसरे को निरस्त कर देंगे जबकि की AB के समांतर घटक
E1 cosθ व E2cosθ एक ही दिशा में होने के कारण जुड़ जाएंगे अतः बिंदु P पर विद्युत द्विध्रुव के कारण परिणामी विद्युत क्षेत्र की तीव्रता
E = E1 cosθ + E2cosθ
= q /4πε₀.k(r² + l²)cosθ + q /4πε₀k.(r² +l²)cosθ
=q /4πε₀k.(r² + l²) {2cosθ }
(चित्र a से) , cosθ = OA/AP = l / (r² +l²)½
अतः E = 2ql / 4πε₀k.(r² +l²)3/2
हम जानते हैं कि p = 2ql
इसलिए
E = P / 4πε₀k.(r² +l²)3/2
यदि l का मान r की अपेक्षा बहुत कम हो तो l² का मान r² की तुलना में नगर में मान सकता है। .
E = P / 4πε₀k.(r² +l²)3/2.
E = P /4πε₀r³ न्यूटन /कूलॉम
इस प्रकार निरीक्षण स्थिति में विद्युत क्षेत्र E की दिशा धन आवेश से ऋण आवेश की ओर जाती है।
प्रश्न 3 : एकसमान विद्युत क्षेत्र में स्थित विद्युत वितरण पर लगने वाले बल -युग्म के आघूर्ण के लिए वंजक प्राप्त कीजिए ।
उत्तर : एक समान विद्युत क्षेत्र में स्थित विद्युत द्विध्रुव पर बल -युग्म – माना AB विद्युत द्विध्रुव एक समान विद्युत क्षेत्र में क्षेत्र की दिशा से θ कोण बनाते हुए रखा है।
मानव विद्युत द्विध्रुव के Aसिरे पर तथा सिरे पर +q आवेश तथा एक दूसरे से 2l दूरी पर स्थित है
।विद्युत क्षेत्र के कारण आवेश +q पर एक बल
{F= qE )क्षेत्र की दिशा में तथा आवेश -q पर उतना ही बल{F= qE ) क्षेत्र की विपरीत दिशा में लगता है।
क्योंकि यह दोनों बोल एक दूसरे के बराबर विपरीत तथा समांतर है बताइए बल युग्म बनाते हैं जो विद्युत द्विध्रुव को घूमर विद्युत क्षेत्र की दिशा में लाने का प्रयत्न करता है ।
इसे τ से प्रदर्शित करते हैं ।
अतः इस प्रत्यय नयन बल युग्म आघूर्ण
τ = एक बल का परिमाण × दोनों बाल की क्रिया रेखाओं के बीच की लंबवत दूरी
= F × AC = 2lsinθ
= qE × 2lsinθ
=2qElsinθ
τ. = PEsinθ. ( P = 2ql )
यदि विद्युत द्विध्रुव विद्युत क्षेत्र के लंबवत रखा हो तो
( θ =90°तब sin 90° = 1 ) विद्युत द्विध्रुव पर लगने वाला बल युग्म अधिकतम होगा । यह अधिकतम मान τ.max होता है।

बिंदु की आवेश +q से दूरी (r-l)और आवेश -q से दूरी (r+l) है यदि इनके संगत तीव्रताएं क्रमशःE1 व E2 हो तो
+q आवेश के कारण बिंदु P पर विद्युत क्षेत्र की तीव्रता
E1 = q /4πε₀.(r – l)². ( A →P दिशा में)
आवेश-q के कारण बिंदु Pपर विद्युत क्षेत्र की तीव्रता
E2 = q /4πε₀.(r+ l)². (P→B दिशा में)
पता बिंदु पर विद्युत द्विध्रुव के कारण परिणामी विद्युत क्षेत्र की तीव्रता
E = E1-E2
= q /4πε₀.k(r – l)². – [q /4πε₀k.(r+ l)².]
= q 4rl/4πε₀k.(r² – l²)².
क्योंकि (P=2ql)
= 2Pr/4πε₀k.(r² – l²)².
E= 2Pr/4πε₀k.(r² – l²)².
यदि l का मान r की अपेक्षा बहुत कम हो तो का l² मान r² तुलना में नगण्य माना जाता है।
E= 2Pr/4πε₀k.(r²)².
E= 2P/4πε₀k.(r³)न्यूटन /कूलॉम
यदि विद्युत द्विध्रुव निर्वात में रखा है, तब K=1 रखने पर बिंदु P पर विद्युत क्षेत्र की तीव्रता
E= 2P/4πε₀k.(r³) न्यूटन /कूलॉम
इस प्रकार अच्छी स्थिति में विद्युत क्षेत्र की दिशा ऋण आवेश से धनावेश की दिशा ओर होती है।
प्रश्न5: स्थिर विद्युत की में गैस का प्रमेय लिखिए। समविभव पृष्ठ से आप क्या समझते हैं ? सामान आवेश घनत्व की दो विद्युत विरोधी प्लेट चित्र अनुसार रखी है बिंदु P एवं Q पर विद्युत क्षेत्र की तीव्रता ज्ञात कीजिए ।

उत्तर: दोनों प्लेटो पर आवेश घनत्व समान है अतः इसके कारण विद्युत क्षेत्र की तीव्रता का परिमाण समान होगा अतः
| E1|=|E2| = σ/2ε₀.
चित्र अनुसार – बिंदु P पर परिणामी विद्युत क्षेत्र की तीव्रता
E= E1 + E2
= σ/2ε₀.+ σ/2ε₀. = σ/ε₀.
बिंदु Q पर परिणामी विद्युत क्षेत्र
E= E1 – E2
= σ/2ε₀.- σ/2ε₀. = 0दोनों प्लेटो पर आवेश घनत्व समान है अतः इसके कारण विद्युत क्षेत्र की तीव्रता का परिमाण समान होगा अतः
| E1|=|E2| = σ/2ε₀.
चित्र अनुसार – बिंदु P पर परिणामी विद्युत क्षेत्र की तीव्रता
E= E1 + E2
= σ/2ε₀.+ σ/2ε₀. = σ/ε₀.
बिंदु Q पर परिणामी विद्युत क्षेत्र
E= E1 – E2
= σ/2ε₀.- σ/2ε₀. = 0
प्रश्न 6 वैद्युत क्षेत्र की तीव्रता की परिभाषा एवं मात्रक लिखिए।
उत्तर : वैद्युत क्षेत्र की तीव्रता “वैद्युत क्षेत्र में किसी बिन्दु पर रखे परीक्षण आवेश पर लगने वाले वैद्युत बल तथा परीक्षण आवेश के अनुपात को उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता कहते हैं।” इसका मात्रक न्यूटन/कूलॉम है।
माना वैद्युत क्षेत्र में किसी बिन्दु पर रखे परीक्षण आवेश q० पर लगने वाला बल →F है तो तो उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता
E = F / qo
इसकी दिशा धनावेश पर कार्यरत बल की दिशा में
प्रश्न 7: निम्नांकित चित्र में a सेमी भुजा वाले वर्ग के चारों कोनों पर चार बिंदु आवेश रखे गए हैं वर्ग के केंद्र O पर विद्युत क्षेत्र का परिमाण व दिशा ज्ञात कीजिए।
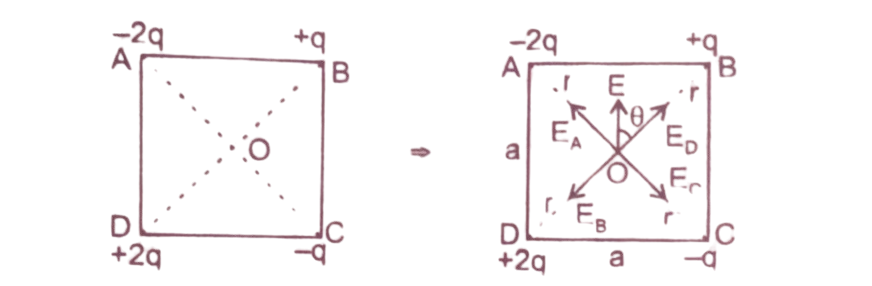
उत्तर : वर्ग की भुजा = a , केंद्र O से दूरी= r सेमी
अतः (2r)² = a² + a² = r = a/√2 सेमी।
चित्रा से विद्युत क्षेत्र की तीव्रता EA= ED = 2q/4πε₀r²
तथा विद्युत क्षेत्र की तीव्रता EB =EC = q/4πε₀r²
परिमानी तीव्रता E1 = EA – EC = q/4πε₀r²(O→A)
E2 = ED – EB = q/4πε₀r² ( O→B)
अतः बिंदु पर परिणामी विद्युत क्षेत्र की तीव्रता
E =√(E1)²+(E2)² = E1√2
= 2 √2q / 4πε₀a²
दिशा θ =tan-¹ (E2/E1) =tan-¹ (1) = 45°
प्रश्न 8- चित्र में दर्शाए अनुसार 10 सेमी भुजा के किसी वर्ग के केंद्र से ठीक सेमी ऊंचाई पर कोई +10 माइक्रो कुलम का आवेश रखा है इस क से गुजरने वाले विद्युत फ्लक्स परिमाण क्या है।
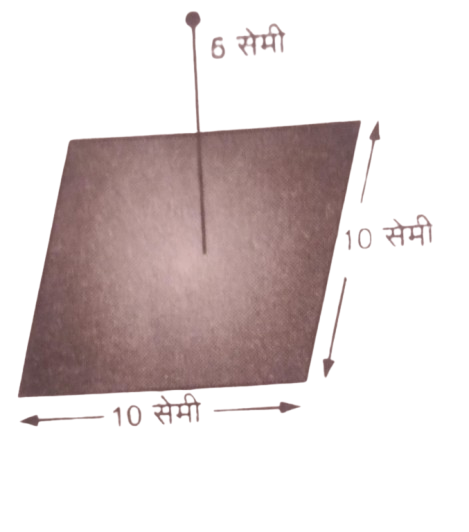
उत्तर : एक ऐसे धन की कल्पना कीजिए जिसका केंद्र व बिंदु है जिस पर आवेश रखा है तथा जिसका एक फलक दिया गया वर्ग है,
गैस के प्रॉमिस है उनके प्रिया से गुजरने वाला फ्लक्स
= 1/ε₀× घन के भीतर कुल आवेश
=q/ε₀
घन के सभी 6 फलक केंद्र के सापेक्ष सामान स्थित है
प्रत्येक फलक से गुजरने वाला फ्लक्स
ØE = q/6ε₀
= 10× 10-⁶/6×8.854×10-¹²
= 1.88 × 10⁵ न्यूटन -मीटर²/कूलॉम
प्रश्न 9: स्थिर विद्युत में गैस के नियम का उल्लेख कीजिए तथा इसकी सहायता से कुलम के नियमों का सूत्र व्यंजक प्राप्त करें ?
उत्तर: गस का नियम नियम – इस नियम के अनुसार किसी बंद कृषि से गुजरने वाले विद्युत फ्लक्स उत्प्रेरक द्वारा परिपथ कल आवेश का 1/ε₀ गुना होता है
ØE = q/ε₀
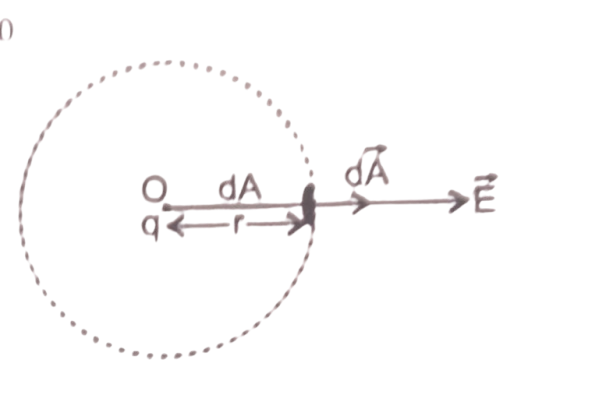
गॉस के नियम से कुलम के नियम की प्राप्ति – एक बिंदु आवेश को केंद्र मानकर उसके चारों ओर अंतरिक्ष का गोलिया पृष्ठ लेते हैं । पृष्ठ पर एक छोटा क्षेत्रफल और dA उपयोग लेते हैं ।
जिस पर विद्युत क्षेत्र वह क्षेत्रफल सदिश दोनों की दिशा सामान त्रिज्या बाहर की ओर है
अतः क्षेत्रफल अवयव से होकर गुजरने वाला विद्युत फ्लक्स
d∅E = EdA cos 0° = EdA
संपूर्ण पृष्ठ से गुजरने वाला विद्युत फ्लक्स
∅E = ∫ E . dA = E ∫ dA
= E. 4πr²: ——–(1)
परंतु गोस के नियम से,
ØE = q/ε₀ —-(2)
समीकरण (1) व (2) से
E. 4πr²= q/ε₀ या E = q/ 4ε₀πr²
यह बिंदु आवेश q. से r दूरी पर विद्युत क्षेत्र की तीव्रता के लिए सूत्र है। यह आवेश q से r दूरी पर परीक्षण आवेश स्थित हो तब उसे पर कार्यरत बाल
F = q°E = qq° / 4πε₀r²
यह गुलाम का नियम है ।
प्रश्न 10- वैद्युन द्विध्रुव तथा वैद्युत द्विध्रुव आपूर्ण को परिभाषित कीजिए। 2 × 10^-8 कुलाम-मीटर द्विधूच आपूर्ण का एक वैद्युत विद्युच 2 x 10^5 मीटर के एकसमान वैद्युत क्षेत्र से 30° पर झुका है। विद्युव की स्थितिज ऊर्जा एवं इस पर कार्यरत बाल-युग्म का आघूर्ण ज्ञात कीजिए।
उत्तर : वैद्युत द्विध्रुव- समान परिमाण एवं विपरीत प्रकृति के दी बिन्दु आवेशी के आत्मत्त निकट रखे होने पर बना निकाय ‘वैद्युत द्विध्रुव ‘ कहलाता है ।
वैद्युत द्विध्रुव आघूर्ण-कसी वैद्युत द्विध्रुव का आघूर्ण उसके किसी एक आवेश के परिमाण तथा आवेशे के बीच की दूरी के गुणनफल के बराबर होता है।
दिया है. p = 2 ×10 ^ – 8 कूलॉम- मीटर
E = 2 × 10^5 वोल्ट- मीटर
θ= 30° , U =? τ = ?
सूत्र। U=-pEcosθ से वैद्युत द्विध्रुव की स्थिति ऊर्जा
U = – 2 ×10 ^ – 8 x 2× 10 ^ 5× cos 30°
U = – 2 × 2 ×√3/2 × 10 ^ – 3
= -2√3×10^-3 जूल ।
सूत्र τ = pEsinθ से निकाय पर कार्यरत बल युग्म आघूर्ण
τ = 2 ×10 ^ – 8 x 2× 10 ^ 5 × sin 30°
= 2 × 2 × 1/2 × 10^-3
τ. = 2 × 10^-3 न्यूटन- मीटर









Pingback: Most important questions for prose class 12
Pingback: Class 12 physics viva Question up board in hindi