Class 12 Physics Chapter 1 Most Important Questions
प्रश्न 1. कूलॉम का वैद्युत बल सम्बन्धी नियम लिखिए।
अथवा कूलॉम का विद्युत बल का नियम क्या है?
Also Read
उत्तर : कूलॉम का नियम- इस नियमानुसार, “दो स्थिर बिन्दु आवेशों के बीच लगने वाला आकर्षण अथवो प्रतिकर्षण बल (F),दोनों आवेशों की मात्राओं ( q1 व q 2 ) के गुणनफल के अनुक्रमानुपाती तथा दोनों आवेशों के बीच की वर्ग के व्युत्क्रमानुपाती होता है।” यह बल दोनों आवेशों को मिलाने वाली रेखा के अनुदिश होता है।
F ∝ q1q2 अथवा
r^2
F = 1 q1q2 न्यूटन
4πε₀. r^2
प्रश्न 2. वैद्युत क्षेत्र की तीव्रता की परिभाषा एवं मात्रक लिखिए।
- उत्तर : वैद्युत क्षेत्र की तीव्रता “वैद्युत क्षेत्र में किसी बिन्दु पर रखे परीक्षण आवेश पर लगने वाले वैद्युत बल तथा परीक्षण आवेश के अनुपात को उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता कहते हैं।” इसका मात्रक न्यूटन/कूलॉम है।
माना वैद्युत क्षेत्र में किसी बिन्दु पर रखे परीक्षण आवेश q० पर लगने वाला बल →F है तो तो उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता
→E =→ F
qo
इसकी दिशा धनावेश पर कार्यरत बल की दिशा में होता है।
प्रश्न 3. यदि किसी 8 सेमी भुजा वाले एक घन के केन्द्र पर 1 कूलॉम आवेश रखा जाए तो घन के किसी फलक से बाहर आने वाले फ्लक्स की गणना कीजिए।
हल : चूँकि घन में 6 फलक होते हैं, अतः वैद्युत फ्लक्स
∅E = q/ε₀.से घन के एक फ्लक्स से बद्ध वैद्युत फ्लक्स
∅E = 1 X 1
6 ε₀.
∅E = __1__
6ε₀.
∅E = 1
6×8.85 ×10^-12
= 1.88 ×10 ^ 10 न्यूटन मीटर² /कूलॉम।
.प्रश्न4 . 7^ N¹⁴नाभिक पर कूलॉम में आवेश की गणना कीजिए।
हल: 7 ^ (N ^ 14) नाभिक में प्रोटॉनों की संख्या = 7
अतः नाभिक पर उपस्थित आवेश q=+ 7e
=+ 7 × 1.6 × 10^-19कूलॉम
= + 1.12 × 10 ^ – 18 कूलॉम ।
प्रश्न 5. 12.5 ×10 ^ 18 इलेक्ट्रॉनों के आवेश की गणना कीजिए।
हल : दिया है n = 12.5 × 10 ^ 18 तथा
e = 1.6 ×10 ^ – 19
कूलॉम आवेश q = ne = 12.5 x 10^18 x 1.6×10-19
= 2 कूलॉम ।
प्रश्न 6. वैद्यत क्षेत्र के फ्लक्स को परिभाषित कीजिए और वैद्यत फ्लक्स का मात्रक लिखिए।
उत्तर : वैद्युत फ्लक्स “किसी वैद्युत क्षेत्र में स्थित किसी काल्पनिक पृष्ठ से, पृष्ठ के लम्बवत् दिशा में गुजरने वाली कुल वैद्युत बलरेखाओं के संख्या को उस पृष्ठ से बद्ध वैद्युत फ्लक्स कहते हैं।
प्रश्न 7. स्थिर वैद्युतिकी में गॉस के नियम का उल्लेख कीजिए ।
अथवा गॉस की प्रमेय क्या है?
उत्तर : गाँस का नियम- इस नियम के अनुसार, “किसी बन्द पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स ∅E उस पृष्ठ के भीतर स्थित कुल आवेश q का 1 /ε₀. गुना होता है।” अर्थात्
∅E = q/ε₀. जहाँ ε₀. निर्वात अथवा वायु की वैद्युतशीलता है।
प्रश्न 8 .वैद्युन द्विध्रुव तथा वैद्युत द्विध्रुव आपूर्ण को परिभाषित कीजिए। 2 × 10^-8 कुलाम-मीटर द्विधूच आपूर्ण का एक वैद्युत विद्युच 2 x 10^5 मीटर के एकसमान वैद्युत क्षेत्र से 30° पर झुका है। विद्युव की स्थितिज ऊर्जा एवं इस पर कार्यरत बाल-युग्म का आघूर्ण ज्ञात कीजिए।
उत्तर- वैद्युत द्विध्रुव- समान परिमाण एवं विपरीत प्रकृति के दी बिन्दु आवेशी के आत्मत्त निकट रखे होने पर बना निकाय ‘वैद्युत द्विध्रुव ‘ कहलाता है ।
वैद्युत द्विध्रुव आघूर्ण-कसी वैद्युत द्विध्रुव का आघूर्ण उसके किसी एक आवेश के परिमाण तथा आवेशे के बीच की दूरी के गुणनफल के बराबर होता है।
दिया है. p = 2 ×10 ^ – 8 कूलॉम- मीटर
E = 2 × 10^5 वोल्ट- मीटर
θ= 30° , U =? τ = ?
सूत्र। U=-pEcosθ से वैद्युत द्विध्रुव की स्थिति ऊर्जा
U = – 2 ×10 ^ – 8 x 2× 10 ^ 5× cos 30°
U = – 2 × 2 ×√3/2 × 10 ^ – 3
= -2√3×10^-3 जूल ।
सूत्र τ = pEsinθ से निकाय पर कार्यरत बल युग्म आघूर्ण
τ = 2 ×10 ^ – 8 x 2× 10 ^ 5 × sin 30°
= 2 × 2 × 1/2 × 10^-3
τ. = 2 × 10^-3 न्यूटन- मीटर
प्रश्न-9-स्थिर वैद्युत बल तथा गुरुत्वाकर्षण बल की तुलना करिए।
उत्तर-दो आवेशित वस्तुओं के बीच गुरुत्वाकर्षण बल तथा वैद्युत बल दोनों कार्य करते हैं-
r दूरी पर स्थित दो द्रव्यमानों के बीच कार्यरत गुरुत्वाकर्षण बल Fg = G m1 m2/r² न्यूटन।
r दूरी पर स्थित दो आवेशों के बीच कार्यरत वैद्युत बल
Fe = q1q2/4πε₀.kr² न्यूटन।
स्थिर वैद्युत बल तथा गुरुत्वाकर्षण बल में समानताएँ – स्थिर वैद्युत बल तथा गुरुत्वाकर्षण बल मे निम्नलिखित समानताएँ है-
(1) दोनों बल, दूरी के व्युत्क्रम वर्ग के नियम का पालन करते हैं।
(ii) दोनों बल, केन्द्रीय एवं संरक्षी बल हैं।
स्थिर वैद्युत बल तथा गुरुत्वाकर्षण बल में असमानताएँ- स्थिर वैद्युत बल तथा गुरुत्वाकर्षण बल में निम्नलिखित असमानताएँ हैं-
(1) वैद्युत बल, आकर्षण तथा प्रतिकर्षण दोनों प्रकृति का हो सकता है जबकि गुरुत्वाकर्षण बल सदैव आकर्षण प्रकृति का ही होता है। वैद्युत बलों की प्रकृति से ज्ञात होता है कि आवेश दो प्रकार के हो सकते हैं, जबकि द्रव्यमान केवल एक ही प्रकार का होता है।
(ii) वैद्युत बल दोनों आवेशों के बीच के माध्यम पर निर्भर करता है जबकि गुरुत्वाकर्षण बल दोनों द्रव्यमानों के बीच के माध्यम पर निर्भर नहीं करता है।
(iii) वैद्युत बल, गुरुत्वाकर्षण बल से बहुत अधिक शक्तिशाली होता है, जैसे दो प्रोटॉनों के बीच लगने वाला वैद्युत बल, उनके बीच लगने वाले गुरुत्वाकर्षण बल से
10³⁶ गुना अधिक होता है, जबकि दो इलेक्ट्रॉनों के बीना लगने वाला वैद्युत बल, उनके बीच लगने वाले गुरुत्वाकर्षण बल से 10⁴³ गुना अधिक होता है।
प्रश्न 10- वैद्युत विभव किसे कहते है ?
उत्तर – किसी धन परीक्षण आवेश को अनन्त से वैद्युत क्षेत्र के किसी बिन्दु तक लाने में, वैद्युत बल के विरुद्ध बाह्य स्त्रोत द्वारा प्रति एकांक आवेश पर किए गए कार्य को उस बिन्दु पर वैद्युत विभव कहते हैं।
अथवा
किसी धन परीक्षण आवेश को अनन्त से वैद्युत क्षेत्र के किसी बिन्दु तक लाने में, वैद्युत बल के विरुद्ध बाह्य स्त्रोत द्वारा किए गए कार्य तथा धन परीक्षण आवेश के परिमाण का अनुपात उस बिन्दु पर वैद्युत विभव कहलाता है।
वैद्युत विभव भी एक अदिश राशि है। इसका मात्रक जूल/कूलॉम या वोल्ट है।
1 वोल्ट = 1 जूल/कूलॉम
प्रश्न 11- वैद्युत फ्लक्स किसे कहते है ?
उत्तर – वैद्युत क्षेत्र में किसी बिन्दु पर क्षेत्र के अभिलम्बवत् रखे एकांक क्षेत्रफल ‘से गुजरने वाली वैद्युत बल-रेखाओं की संख्या उस बिन्दु पर वैद्युत क्षेत्र की प्रबलता को प्रदर्शित करती है। अतः वैद्युत क्षेत्र के लिए हम एक अन्य राशि को परिभाषित करते हैं, जो किसी पृष्ठ से गुजरने वाली कुल वैद्युत बल-रेखाओं की संख्या को प्रदर्शित करता है, इसे वैद्युत फ्लक्स कहते हैं।
अतः वैद्युत क्षेत्र में स्थित किसी काल्पनिक पृष्ठ से सम्बद्ध वैद्युत फ्लक्स उस पृष्ठ से होकर गुजरने वाली वैद्युत बल-रेखाओं की संख्या की माप है। इसे ‘∅E’ से प्रदर्शित करते हैं।
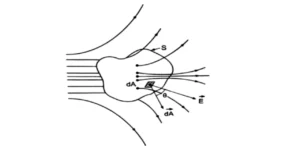
प्रश्न 12 – गॉस की प्रमेय या गॉस का नियम लिखिए।
उत्तर – कार्ल फ्रेडरिच गाँस (Karl Friedrich Gauss) ने किसी बन्द पृष्ठ से होकर गुजरने वाले वैद्युत फ्लक्स तथा पृष्ठ द्वारा परिबद्ध कुल वैद्युत आवेशी के बीच एक परिमाणात्मक सम्बन्ध स्थापित किया, जिसे गाँस की प्रमेय या गाँस का नियम कहते हैं। इस प्रमेय के अनुसार- “किसी बन्द पृष्ठ से गुजरने वाला वैद्युत फ्लक्स उस पृष्ठ द्वारा परिबद्ध (घिरे हुए) कुल वैद्युत आवेश का गुना होता है।” 1/ε₀
यदि किसी बन्द पृष्ठ द्वारा परिबद्ध (घिरा हुआ) कुल आवेश १ हो तो गाँस की प्रमेय के अनुसार उस पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स
∅E = q/ε₀ होता हैं