Class 12 Physics Chapter 2 Important Question Answer in Hindi
प्रश्न 1- वैद्युत द्विध्रुव की अक्षीय रेखा पर वैद्युत विभव का सूत्र लिखिए।
उत्तर – अक्षीय स्थिति में, V = 1/4π€°तथा निरक्षीय स्थिति में, V = 0
Also Read
प्रश्न 2- सम विभव पृष्ठ से क्या तात्पर्य है?
उत्तर : समविभव पृष्ठ-किसी बिन्दु आवेश के चारों ओर खींचा गया वह काल्पनिक पृष्ठ जिसके प्रत्येक बिन्दु पर विभव का मान समान हो समविभव पृष्ठ कहलाता है।
प्रश्न 3– किसी चालक के समविभव पृष्ठ के किसी बिन्दु पर वैद्युत क्षेत्र रेखाएँ पृष्ठ के लम्बवत् क्यों होती हैं?
उत्तर : यदि वैद्युत क्षेत्र समविभव पृष्ठ के लम्बवत् नहीं है तो वैद्युत क्षेत्र का समविभव पृष्ठ के अनुदिश कोई शून्येतर (non-zero) घटक होगा। अतः किसी परीक्षण आवेश को समविभव पृष्ठ पर इस घटक के विरुद्ध गति कराने में कुछ कार्य करना होगा जबकि समविभव पृष्ठ पर परीक्षण आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य शून्य होता है। अतः वैद्युत क्षेत्र एवं वैद्युत बल-रेखाएँ समविभव सतह के लम्बवत् होती हैं।
प्रश्न 4- वैद्युत विभव तथा वैद्युत विभवान्तर से क्या तात्पर्य है? इनके मात्रक लिखिए।
अथवा
वैद्युत विभव की परिभाषा तथा विमा लिखिए।
उत्तर : वैद्युत विभव “वैद्युत क्षेत्र में, किसी परीक्षण घन आवेश (+q⁰) को अनन्त से किसी बिन्दु तक लाने में किए गए कार्य (W) तथा परीक्षण आवेश के अनुपात को उस बिन्दु पर वैद्युत विभव कहते हैं।” यह अदिश राशि है।
माना परीक्षण आवेश q० को अनन्त से वैद्युत क्षेत्र के किसी बिन्दु तक लाने में किया गया कार्य W है तो उस बिन्दु पर वैद्युत विभव V = W/q⁰ है।
इसका मात्रक जूल/कूलॉम अथवा वोल्ट है। इसकी विमा [ML2T-3A-1] है।
वैद्युत विभवान्तर- “वैद्युत क्षेत्र में, किसी परीक्षण धन आवेश (+q0) को एक बिन्दु से दूसरे बिन्दु तक लाने में किए गए कार्य (W) तथा परीक्षण आवेश के अनुपात को उन बिन्दुओं के बीच वैद्युत विभवान्तर कहते हैं।” यह अदिश राशि है।
माना किसी धन परीक्षण आवेश + q⁰ को वैद्युत क्षेत्र के किसी बिन्दु B से बिन्दु A तक ले जाने में क्षेत्र के विरुद्ध W. कार्य करना पड़ता है तथा बिन्दुओं A तथा B के वैद्युत विभव क्रमशः VA तथा VB हैं तो
वैद्युत विभवान्तर VB-VA = W/ q⁰ इसका मात्रक भी जूल/कूलॉम अथवा वोल्ट है।
प्रश्न 5- संधारित्र की धारिता से क्या अभिप्राय है? इसका मात्रक लिखिए।
उत्तर : संधारित्र की धारिता – “किसी संधारित्र की धारिता उसकी वैद्युत आवेश को संग्रहित करने की क्षमता का माप है।” इसे C से प्रदर्शित करते हैं। यदि किसी संधारित्र को q आवेश देने पर उसके प्लेटों के बीच विभवान्तर V उत्पन्न होता है, तो संधारित्र की धारिता C = q/V होती है।
इसका मात्रक कूलॉम/वोल्ट अथवा फैरड (Farad) है। फैरड एक बड़ा मात्रक है, इसलिए व्यवहार में माइक्रोफैरड (µF) और पिकोफैरड (pF) जैसे छोटे मात्रकों का उपयोग किया जाता है।
प्रश्न 6- सिद्ध कीजिए कि किसी वैद्युत द्विध्रुव की अनुप्रस्थ (निरक्षीय) स्थिति में किसी बिन्दु पर वैद्युत विभव शून्य होता है।
उत्तर– वैद्युत द्विध्रुव की निरक्षीय रेखा पर स्थित किसी बिन्दु पर वैद्युत विभव-माना AB वैद्युत द्विध्रुव K परावैद्युतांक के माध्यम में स्थित है, जिसके A सिरे पर +q आवेश A तथा B सिरे पर -q आवेश एक-दूसरे से 2l दूरी पर स्थित हैं (चित्र)। वैद्युत द्विध्रुव के मध्य-बिन्दु 0 से मीटर की दूरी पर निरक्षीय स्थिति में कोई बिन्दु P है, जहाँ पर वैद्युत विभव ज्ञात करना है। संलग्न चित्र से स्पष्ट है कि बिन्दु P की q तथा- qदोनों आवेशों से दूरी √(r² + l²) के बराबर है।
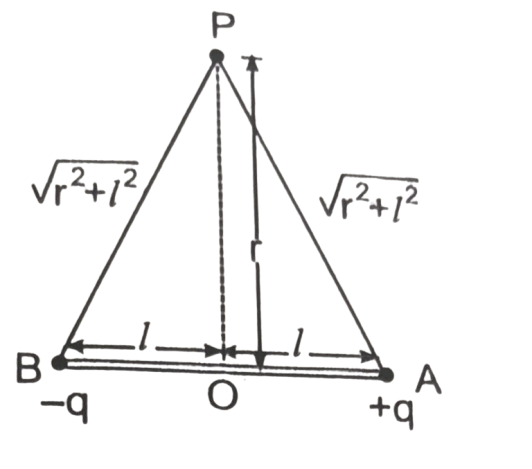
अतः आवेश q के कारण बिन्दु P पर वैद्युत विभव
V1 = q/4π€°K(r² + l²)½वोल्ट
आवेश – q के कारण बिन्दु P पर वैद्युत विभव
V2 = -q/4π€°K(r² + l²)½वोल्ट
बिन्दु P पर परिणामी वैद्युत विभव
V = V1 + V2
V = q/4π€°K(r² + l²)½ – q/4π€°K(r²
+ l²)½
V=0
उत्तर : समविभव पृष्ठ-वैद्युत क्षेत्र में स्थित ऐसा पृष्ठजिसके प्रत्येक बिन्दु का वैद्युत विभव समान होता है, समविभव पृष्ठ कहलाता है।
प्रश्न 7- समविभव पृष्ठ से क्या तात्पर्य है? इसकी महत्त्वपूर्ण विशेषताएँ क्या हैं? आवेश दो खोखले संकेन्द्रीय गोलों पर जिनकी त्रिज्याएँ r1तथा r₂(r₁ > r₂) हैं, इस प्रकार से वितरित किया है ताकि उनके आवेश के पृष्ठ घनत्व समान हों। गोलों के उभयनिष्ठ केन्द्र पर विभव ज्ञात कीजिए। [ Important]
उत्तर : समविभव पृष्ठ-वैद्युत क्षेत्र में स्थित ऐसा पृष्ठजिसके प्रत्येक बिन्दु का वैद्युत विभव समान होता है, समविभव पृष्ठ कहलाता है।

समविभव पृष्ठ की विशेषताएँ – (i) समविभव पृष्ठ पर किसी बिन्दु केआवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य शून्य होता है।
(ii) समविभव पृष्ठ के प्रत्येक बिन्दु पर वैद्युत क्षेत्र की तीव्रता पृष्ठ के लम्बवत् होती है।
(iii) दो समविभव पृष्ठ कभी एक-दूसरे को नहीं काटते हैं, क्योंकि यदि ऐसा होगा तो उनके कटान बिन्दु पर खींचे गए दो अभिलम्ब, उस बिन्दु पर वैद्युत क्षेत्र की दो दिशाओं को प्रदर्शित करेंगे, जोकि असम्भव
है।
माना आवेश Q, दोनों संकेन्द्रीय गोलों पर r1 व r२ में बँट जाता है।
अतः q1 + q2 = Q —(1)
दोनों गोलों पर आवेश पृष्ठ घनत्व. समान है, अतः
σ = q/ 4πr1² =q/ 4πr2²
याq1 /q2 = r1²/r2²
q 1 = r1²/r2² .q 2 —-(2)
समीकरण (2) से समीकरण(1) में मान रखने पर,
q2 = (Q r2²/(r1 ^ 2 + r2 ^ 2)
गोलों के उभयनिष्ठ केन्द्र पर विभव
V = 1/(4π€°) (Q(r1+ r2)/(r1^ 2 + r2 ^ 2)
प्रश्न 8- सिद्ध कीजिए कि किसी वैद्युत द्विध्रुव की अक्षीय स्थिति में किसी बिन्दु पर वैद्युत विभव V = 1/4πε₀ p/r² होता है।
उत्तर- वैद्युत द्विध्रुव की अक्षीय रेखा पर स्थित किसी बिन्दु पर वैद्युत विभव- माना AB एक वैद्युत द्विध्रुव है जो K परावैद्युतांक के माध्यम में स्थित है। इसके A सिरे पर +q आवेश तथा B सिरे पर -q आवेश एक-दूसरे से 2l दूरी पर स्थित हैं। वैद्युत द्विध्रुव के मध्य-बिन्दु O से r दूरी पर अक्षीय स्थिति में कोई बिन्दु P है, जहाँ पर वैद्युत विभव ज्ञात करना है।
आवेश +q के कारण बिन्दु P पर वैद्युत विभव:
बिन्दु P की आवेश +q से दूरी (r – l) है।
अतः V₁ = 1/(4πε₀K) q/(r – l)
आवेश -q के कारण बिन्दु P पर वैद्युत विभव:
बिन्दु P की आवेश -q से दूरी (r + l) है।
अतः V₂ = 1/(4πε₀K) (-q)/(r + l)
बिन्दु P पर परिणामी वैद्युत विभव:
V = V₁ + V₂
V = 1/(4πε₀K) [q/(r – l) – q/(r + l)]
V = q/(4πε₀K) [(r + l – (r – l))/((r – l)(r + l))]
V = q/(4πε₀K) [2l/(r² – l²)]
V = 1/(4πε₀K) (q 2l)/(r² – l²)
चूँकि वैद्युत द्विध्रुव आघूर्ण p = q 2l होता है,
अतः V = 1/(4πε₀K) p/(r² – l²)
यदि द्विध्रुव बहुत छोटा हो, अर्थात् l << r, तो l² को r² की तुलना में नगण्य माना जा सकता है।
इस स्थिति में, V = 1/(4πε₀K) p/r²
यदि माध्यम वायु या निर्वात हो, तो K = 1।
अतः V = 1/(4πε₀) p/r²
यही वैद्युत द्विध्रुव की अक्षीय स्थिति में वैद्युत विभव का अभीष्ट सूत्र है।
प्रश्न 8- सिद्ध कीजिए कि किसी वैद्युत द्विध्रुव की अक्षीय स्थिति में किसी बिन्दु पर वैद्युत विभव V = 1/4πε₀ p/r² होता है।
उत्तर– वैद्युत द्विध्रुव की अक्षीय रेखा पर स्थित किसी बिन्दु पर वैद्युत विभव- माना AB एक वैद्युत द्विध्रुव है जो K परावैद्युतांक के माध्यम में स्थित है। इसके A सिरे पर +q आवेश तथा B सिरे पर -q आवेश एक-दूसरे से 2l दूरी पर स्थित हैं। वैद्युत द्विध्रुव के मध्य-बिन्दु O से r दूरी पर अक्षीय स्थिति में कोई बिन्दु P है, जहाँ पर वैद्युत विभव ज्ञात करना है।
आवेश +q के कारण बिन्दु P पर वैद्युत विभव:
बिन्दु P की आवेश +q से दूरी (r – l) है।
अतः V₁ = 1/(4πε₀K) q/(r – l)
आवेश -q के कारण बिन्दु P पर वैद्युत विभव:
बिन्दु P की आवेश -q से दूरी (r + l) है।
अतः V₂ = 1/(4πε₀K) (-q)/(r + l)
बिन्दु P पर परिणामी वैद्युत विभव:
V = V₁ + V₂
V = 1/(4πε₀K) [q/(r – l) – q/(r + l)]
V = q/(4πε₀K) [(r + l – (r – l))/((r – l)(r + l))]
V = q/(4πε₀K) [2l/(r² – l²)]
V = 1/(4πε₀K) (q 2l)/(r² – l²)
चूँकि वैद्युत द्विध्रुव आघूर्ण p = q 2l होता है,
अतः V = 1/(4πε₀K) p/(r² – l²)
यदि द्विध्रुव बहुत छोटा हो, अर्थात् l << r, तो l² को r² की तुलना में नगण्य माना जा सकता है।
इस स्थिति में, V = 1/(4πε₀K) p/r²
यदि माध्यम वायु या निर्वात हो, तो K = 1।
अतः V = 1/(4πε₀) p/r²
यही वैद्युत द्विध्रुव की अक्षीय स्थिति में वैद्युत विभव का अभीष्ट सूत्र है।
प्रश्न 9- समान्तर प्लेट संधारित्र की धारिता के लिए सूत्र का निगमन कीजिए। इसकी धारिता को किस प्रकार बढ़ाया जा सकता है?
अथवा
एक समान्तर प्लेट संधारित्र की धारिता का सूत्र स्थापित कीजिए।
[2026 Expected]
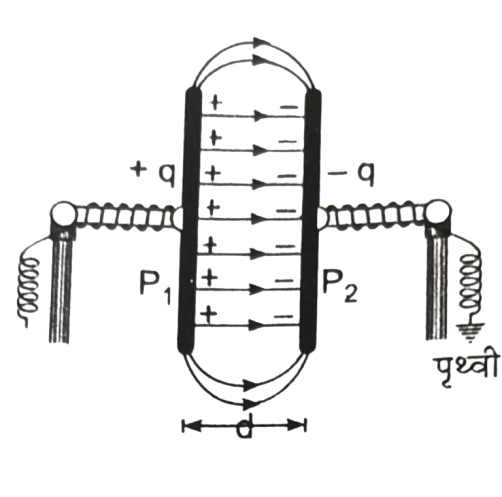
उत्तर – परावैद्युत ध्रुवण- बाह्य वैद्युत क्षेत्र में परावैद्युत पदार्थों में धनावेशों तथा ऋणावेशों के आपेक्षिक विस्थापित होने की घटना को परावैद्युत पदार्थों का वैद्युत ध्रुवण कहते हैं।
समान्तर प्लेट संधारित्र की धारिता का व्यंजक-दो समतल तथा समान्तर धातु की प्लेटों एवं उनके बीच स्थित वैद्युतरोधी माध्यम से बने निकाय को समान्तर प्लेट संधारित्र कहते हैं।
माना P1 व P 2 घातु की दो समतल प्लेटें हैं, जिनके बीच की दूरी d तथा प्रत्येक प्लेट का क्षेत्रफल A है। माना प्लेटों के बीच भरे माध्यम का परावैद्युतांक K है। जब प्लेट P1 को + q आवेश दिया जाता है तो प्लेट P2 पर प्रेरण के कारण – q आवेश उत्पन्न हो जाता है। चूंकि प्लेट P2 पृथ्वी से जुड़ी है इसीलिए इसके बाह्य का +q आवेश P1,. P2 पृथ्वी से आने वाले इलेक्ट्रॉनों द्वारा निरावेशित हो जाता है। इस प्रकार प्लेटों P₁ व P2 पर बराबर तथा विपरीत प्रकार के आवेश होंगे।
प्रत्येक प्लेट पर आवेश का पृष्ठ घनत्व σ =q\A
प्लेटों के बीच किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता E = σ/ K€⁰
σ का मान रखने पर, वैद्युत क्षेत्र की तीव्रता
E= q/AK€⁰ ——(1)
माना दो प्लेटों के बीच विभवान्तर V वोल्ट है, तब प्लेटों के बीच वैद्युत क्षेत्र की तीव्रता E = V / d
अथवा V = Ed
समीकरण (1) से E का मान रखने पर
V = (qd)/(K€°A)
अतः संधारित्र की धारिता C = q/v
C= qd/K€°A.
= KA€° /d फैरड
समान्तर प्लेट संधारित्र की धारिता निम्नलिखित तथ्यों पर निर्भर करती है-
1. प्लेटों के क्षेत्रफल A पर- C × A अर्थात् धारिता प्लेटों के क्षेत्रफल के अनुक्रमानुपाती होती है, अतः संधारित्र की धारिता बढ़ाने के लिए प्लेटों का क्षेत्रफल A अधिक होना चाहिए अर्थात् प्लेटें बड़े क्षेत्रफल की लेनी चाहिए।
2. प्लेटों के बीच की दूरी d -C × 1 / d अर्थात् धारिता प्लेटों के बीच की दूरी के व्युत्क्रमानुपाती होती है, अतः संधारित्र की धारिता बढ़ाने के लिए प्लेटों के बीच की दूरी d कम होनी चाहिए अर्थात् प्लेटें एक-दूसरे के समीप रखनी चाहिए।
3. प्लेटों के बीच के माध्यम K पर – C ~ K अर्थात् धारिता माध्यम के परावैद्युतांक के अनुक्रमानुपाती होती है, अतः संधारित्र की धारिता बढ़ाने के लिए प्लेटों के बीच ऐसा माध्यम अर्थात् पदार्थ रखना चाहिए जिसका परावैद्युतांक (K) अधिक हो।
प्रश्न 10- संधारित्र से क्या तात्पर्य है?
उत्तर : संधारित्र-संधारित्र किसी भी प्रकार के दो ऐसे चालकों का युग्म है जो कि एक-दूसरे के समीप हों, जिन पर बराबर व विपरीत आवेश हों तथा जिसकी एक प्लेट पृथ्वी से जुड़ी हो।
प्रश्न 11. संधारित्रों के उपयोग लिखिए।
उत्तर : संधारित्रों के उपयोग- (1) आवेश का संचय करने में, का संचय करने में तथा (3) वैद्युत उपकरणों में।
प्रश्न 12. किसी संधारित्र की धारिता की परिभाषा व मात्रक लिखिए।
उत्तर : संधारित्र की धारिता – “संधारित्र की एक प्लेट को दिए गए आवेश तथा दोनों प्लेटों के बीच उत्पन्न विभवान्तर के अनुपात को संधारित्र की धारिता कहते हैं।” इसका मात्रक फैरड है।
—–EXAM HACK FOR STUDENTS ——-
1- यूपी बोर्ड परीक्षा में सफलता के लिए सिलेबस को अच्छी तरह समझे और नियमित अभ्यास करें ।
2- पढ़ाई कि योजना बनाए जिसमे हर विषय के लिए समय हो समझो टॉपिक पर ज्यादा फॉक्स करे।
3- पेपर में पहले आसान सवाल हल करें सभी प्रश्नों के उत्तर दें बिन कोई छोड़ें।
4- परीक्षा में व्हाइटनर(whitener) का उपयोग न करें केवल काला(black), नीला (blue) पेन का उपयोग करें ।